29-05-2014، 9:09
پژوهشگران موفق شدهاند با ایجاد چگالیدهی بوز-انیشتین (BEC) از فوتونها٬ اثرات عیرعادی آن را برملا کنند. این پژوهش به عنوان مثالی نادر از یک گاز کوانتومی در هنگرد بندادی بزرگ (grand canonical ensemble) محسوب میشود. براساس نتایج این تحقیق٬ تعدادی از ذرات در چگالیدهی بوز-انشتین میتوانند افتوخیزهای قوی داشته باشند. این محققان نشان دادهاند امکان این وجود دارد که یک BEC طوری ساخته شود که تعداد ذرات در آن پایسته نباشد؛ نتیجهای که به پرسش دیرینهی فیزیک آماری میپردازد.
در معروفترین نوع چگالیدهی بوز-انشتین (BEC) اتمهای یکسان حضور دارند. اگر چنین مادهای را تا دماهای بسیار پائین سرد کنیم٬ اتمهای تشکیلدهندهی آن به شکل جمعی دریک حالت کوانتومیِ تکذرهای قرار میگیرند و یک موج-مادهی غولپیکر را تشکیل میدهند. BECها اما میتوانند از دیگر انواع بوزونها (شامل پولاریتونها و فوتونها) نیز تشکیل شوند که برخلاف اتمها٬ میتوان آنها را در یک تلهی ایزوله (در داخل مادهای که تولید شدهاند) ایجاد و یا از بین برد. اکنون پژوهشگران از اثرات آماری غیرمعمول در یک BEC که ذرات و انرژی را با چنان مادهای تبادل میکند٬ پرده برداشتهاند. جولیان اشمیت (Julian Schmitt) و همکارانش از دانشگاه بُنِ آلمان یک BEC از فوتونها را در داخل حمامی از مولکولهای رنگیِ تحریکپذیر تولید کردهاند. این مولکولها هم به عنوان «مخزنی» از فوتونها و هم به عنوان یک حمام گرم عمل میکند. این تحقیق نشان میدهد افتوخیزهای ذرات در این چگالیده٬ توانسته کسر قابل توجهی از تعداد کل ذرات را دربرگیرد(۱). آزمایش آنان که در مجلهی فیزیکال ریویو لیترز انتشار یافته مثالی نادر از یک گاز کوانتومی در هنگرد بندادی بزرگ (grand-canonical ensemble) مکانیک آماری به حساب میآید.
چگالیدههای بوز-انشتین همانند بسیاری از سیستمهایی که حاوی تعدادی زیادی از ذرات هستند٬ به شکل آماری توصیف میشوند. هنگردهای آماری مختلف (تعداد زیادی از ذراتی که تحت شرایط ترمودینامیکی ویژه مهیا میشوند) میتوانند از خواص فیزیکی مشابهی برخوردار باشند. اما نسلهای مختلفی از فیزیکپژوهان بر سر این موضوع بحث کردهاند که چنان رفتاری نبایستی در مورد افتوخیزهای ذرات در چنین چگالیدههایی صادق باشد(۲). بویژه وقتی یک BEC بتواند هم گرما و هم ذرات را با یک مخزن گرمایی تبادل کند(شرایطی که از آن بعنوان «هنگرد بندادی بزرگ» یاد میشود) نظریهپردازان یک افتوخیز «فاجعهبار» را پیشبینی کردهاند. طوریکه افتوخیزها در تعدادی از این ذرات به بزرگی تعداد کل ذرات موجود در چگالیده است. برعکس٬ تحت شرایط «هنگرد بندادی» (که در آن تنها گرما و نه ذرات میتوانند با یک مخزن تبادل شوند) تعداد کل ذرات بایستی پایسته مانده و افتوخیزهای بزرگ رخ نمیدهند. به شکل مشابه٬ افتوخیزهای بزرگ نبایستی در یک هنگرد «میکروکانونی» رخ رهند؛ هنگردی که در آن هم انرژی و هم ذرات پایسته میمانند.
تاکنون فیزیکدانان تجربی این اثرات آماری وابسته به هنگرد در BECها را مشاهده نکرده بودند. یک دلیل عملی بر این ادعا وجود دارد: در مورد یک چگالیدهی اتم٬ گاز اتمی بایستی از محیط پیرامونش ایزوله باشد تا بتوان آن را تا دماهای پایین سرد کرد. بنابراین چنان BECهایی را معمولاً میتوان تحت شرایط هنگرد میکروکاننی ایجاد کرد(۲). در اصل بایستی امکان مشاهدهی افتوخیزهای ذرات در BECهایی از اکسیتون-پلاریتون وجود داشته باشد. چنان چگالیدههایی در سیستمهای حالت-جامد میتوانند رخ دهند. اما٬ هم کنترل صحیحِ مخزن و هم اندازهگیری دقیق افتوخیزهای سریع (در مقیاس پیکوثانیه) به دشواری به اثبات رسیده است. نهایتاً این سوال پیش میآید که آیا امکان این وجود دارد که یک BEC تحت شرایط هنگرد بندادی بزرگ تشکیل شود.
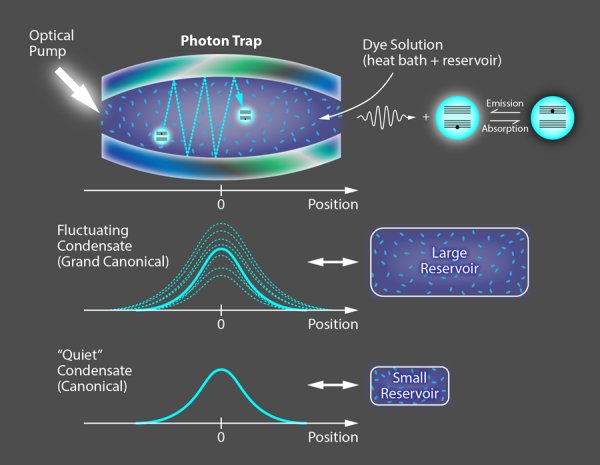
گروه بن نشان دادهاند که در حقیقت این شرایط را میتوان در BECای از فوتونها ممکن ساخت؛ سیستمی که آنها چندین سال پیش تولید کردهاند(۵). در این سیستم٬ فوتونهایی را با استفاده از یک لیزر برای تحریک مولکولهای رنگی در داخل یک کاواک اپتیکی با آینههایی در دو انتهای آن ایجاد کردهاند (شکل ۱ قسمت بالا). اگر این دو آینه کاملاً صاف باشند تنها حرکت فوتونها در جهت طولی (در جهت عمود بر آینهها) کوانتیده شده و فوتونها برای حرکت در جهت عرضی آزاد خواهند بود؛ رفتاری که معادل رفتار فوتونهایی است که جرم موثر دارند. اما آینهها در دستگاه اشمیت و همکارانش اندکی انحنا یافته است. این کار باعث میشود تا محدودشدگی (Confinemet) بیشتری فراهم شود و حتی حرکت عرضی فوتونها نیز کوانتیده گردد. در نتیجه٬ فوتونهای به دام افتاده همچون یک گاز دوبعدی از بوزونهای پرجرم در پتانسیل هارمونیک رفتار میکند. مولکولهای رنگی در آزمایش اشمیت و همکارانش با چنان دقتی انتخاب میشوند که در زمان تحریکشدن٬ فوتونهایی را گسیل کنند که انرژی آنها با انرژی زیرترازهای یک مد طولی کاواک ویژه (در این مورد ۲.۱ الکترونولت) مشابه باشد. برای ایجاد یک BEC ٬ بایستی طول موج دوبروی بوزونها٬ همپوشانی چشمگیری باهم داشته باشند که این اتفاق برای اتمها تنها در دماهای زیرمیکرو کلوین رخ میدهد. اما جرم موثر فوتونهای کاواکِ موردنظر در آزمایش اشمیت و همکارانش چندین مرتبه کوچکتر از اندازهی یک اتم هیدروژن است؛ چیزی که باعث میشود BECی فوتونها در دمای اتاق تشکیل شود.
در این سیستم مولکولهایی که در کاواک حضور دارند قادرند تا فوتونها را هم جذب کنند و هم گسیل. بنابراین هم به عنوان یک مخزن ذره عمل میکنند و هم حمام گرم. گروه بن از اسبابی موسوم به هانبری-براون-توئیس (Hanbury-Brown-Twiss) برای اندازهگیری افتوخیزهای متوسط δn0 حول مقدار میانگین n0 فوتونهای چگالیده استفاده میکنند. پژوهشگران میتوانند نوع مخزن (و از اینرو شرایط هنگردیِ آماری) را تغییر دهند. آنان این کار را با میزانسازیِ تعداد مولکولهای رنگی و تغییر در ترکیب شیمیایی آنها (به منظور تغییر فرکانس گذار این مولکولها) انجام میدهند. در حقیقت این محققان٬ با افزایش اختلاف فرکانس بین فرکانس مولکولهای رنگی و فرکانس مد کاواک٬ جفتشدگی دمایی بین فوتونهای کاواک و مخزن را کاهش میدهند. این پارامترهای کنترلی آنان را قادر میسازد تا اندازهی موثر مخزن را به بیش از سه برابر تغییر دهند. تاثیر اندازهی مخزن بر روی ویژگیهای افتوخیزی جالب است: وقتی ۳۰ درصدِ تمامی فوتونهای درون کاواک چگالیده میشوند و مخزن در بزرگترین حالت خود قرار دارد٬ این پژوهشگران یک تعداد افتوخیز نسبی δn/0n0≃80% (شکل یک- بخش مرکزی) را مشاهده میکنند. این «آشفتگی» بزرگ و غیرعادی برای چنان فاجعهی افتوخیزیِ بندادیِ بزرگ انتظار میرود. اگر آنها اندازهی مخزن را کاهش دهند٬ برای کسر چگالیدهگیِ یکسان٬ افتوخیز نسبی (δn0 /n0) تدریجاً به سمت صفر میرود (شکل یک-بخش پائینی).
همانطور که اشمیت و همکارانش به آن دست یافتهاند٬ توزیع فوتونها در سیستم موردنظر به ازای مخزنی با اندازهی دلخواه٬ با مدل سادهی آماری توافق دارد. یک فرض اصلی برای این مدل آماری (۶) این است که در حالت پایا٬ تعداد مولکولهایی که به شکل اپتیکی تحریک شدهاند (یعنی تعداد فوتونهای داخل مخزن) بعلاوهی فوتونهای داخل کاواک ثابت است. برای آنکه چنین ادعایی صحت داشته باشد٬ بایستی میراییِ تحریکات مولکولی در محلول رنگی پائین باشد؛ همانگونه که در آزمایش اشمیت و همکارانش نیز چنین است. برای یک مخزن به حد کافی بزرگ٬ آمار هنگرد بندادی بزرگ هم در آزمایش و هم در تئوری بدست میآید.
اینکه آیا ممکن است فوتونهایی ساخته شوند که یک BEC واقعی را تشکیل دهند٬ منشا برخی بحثها بوده است. دلیل وجود چنان بحثهایی این است که حتی زمانیکه آینهها در یک کاواک اپتیکیِ بازتابکنندهی بسیار خوب قرار داشته باشند٬ فوتونها طولعمر محدودی دارند. اشمیت و همکارانش برای جبران چنین نقطهضعفی به تحریک مدام فوتونهای جدید در آزمایششان نیاز دارند. در نگاه اول به نظر میرسد یک سیستمی که به شکل مدام پمپاژ میشود نمیتواند هرگز به تعادل گرمایی برسد؛ در مقالاتی که دربارهی تولید نور لیزری فوتونی و چگالش مطالعاتی انجام شده(۷و۸و۹) بر روی این موضوع بحث شده است. اما نظریهی غیرتعادلی اخیر (۹) نشان داده که حداقل برای سیستمهای رنگی (همچون سیستمی که در آزمایش اشمیت و همکارانش استفاده شده) افزایش طولعمر فوتونهای کاواک٬ به تشکیل یک چگالش گرماداده شده و شبه بوز-انشتین از فوتونها میانجامد. نکتهی اصلی این است که فوتونها میتوانند با دمای ارتعاشیِ ناشی از مولکولهای رنگی٬ در طول جذب و بازگسیلِ فوتونهای مکرر به تعادل گرمایی برسند. مادامیکه این فرآیندها سریعتر از زمانی که طول میکشد تا یک فوتون در کاواک میرا شود٬ انجام گردد٬ تعادل گرمایی قابل دسترسی خواهد بود.
اشمیت و همکارانش اساساً «مهندسیِ مخزن» را اجرا کردهاند: این گروه چنان سیستم آزمایشگاهی را طراحی کردهاند که به واسطهی آن به افتوخیزهای یک چگالیدهی بوز-انشتین تسلط پیدا میکنند. فیزیکِ موجود در سیستم آنها را میتوان در دیگر سیستمهای بسذرهای (همچون یک چگالیدهگی اکسیتون-پلاریتون) نیز اعمال کرد. این کار همچنین در درک شرایط غیرتعادلی با آمار غیرحرارتی مفید باشد. مسیر جذابی که میتواند در آینده دنبال شود این خواهد بود که ببینیم برهمکنشهای بین فوتونها در کاواک٬ ویژگیهای آماریِ BEC فوتونی را چگونه تحت تاثیر قرار میدهد. به ویژه٬ این اثرات ممکن است به انتشار ابرشارهی فوتونی و نیز به فیزیکِ سیستمهای فوتونی که قویاً همبسته هستند٬ مربوط شود.
در معروفترین نوع چگالیدهی بوز-انشتین (BEC) اتمهای یکسان حضور دارند. اگر چنین مادهای را تا دماهای بسیار پائین سرد کنیم٬ اتمهای تشکیلدهندهی آن به شکل جمعی دریک حالت کوانتومیِ تکذرهای قرار میگیرند و یک موج-مادهی غولپیکر را تشکیل میدهند. BECها اما میتوانند از دیگر انواع بوزونها (شامل پولاریتونها و فوتونها) نیز تشکیل شوند که برخلاف اتمها٬ میتوان آنها را در یک تلهی ایزوله (در داخل مادهای که تولید شدهاند) ایجاد و یا از بین برد. اکنون پژوهشگران از اثرات آماری غیرمعمول در یک BEC که ذرات و انرژی را با چنان مادهای تبادل میکند٬ پرده برداشتهاند. جولیان اشمیت (Julian Schmitt) و همکارانش از دانشگاه بُنِ آلمان یک BEC از فوتونها را در داخل حمامی از مولکولهای رنگیِ تحریکپذیر تولید کردهاند. این مولکولها هم به عنوان «مخزنی» از فوتونها و هم به عنوان یک حمام گرم عمل میکند. این تحقیق نشان میدهد افتوخیزهای ذرات در این چگالیده٬ توانسته کسر قابل توجهی از تعداد کل ذرات را دربرگیرد(۱). آزمایش آنان که در مجلهی فیزیکال ریویو لیترز انتشار یافته مثالی نادر از یک گاز کوانتومی در هنگرد بندادی بزرگ (grand-canonical ensemble) مکانیک آماری به حساب میآید.

دیدن لینک ها برای شما امکان پذیر نیست. لطفا ثبت نام کنید یا وارد حساب خود شوید تا بتوانید لینک ها را ببینید.
شکل ۱) چگالیدهی بوز-انشتین از فوتونها. (قسمت بالا) اشمیت و همکارانس BECای از فوتونی را با پمپاژ اپتیکی که به منظور تحریک مولکولهای رنگی در یک کاواک اپتیکی بکار می رود را تولید کردهاند. این مولکولهای پیرامونی به عنوان یک حمام گرم و یک مخزن ذرات عمل میکنند. (بخش مرکزی) وقتی اندازهی موثر مخزن به حد کافی بزرگ باشد٬ این اسباب شرایط هنگرد بندادی بزرگ را فراهم میکنند. اشمیت و همکارانش افتوخیزهای بزرگی را در تعدادی از ذرات موجود در این چگالیده مشاهده کردهاند. (بخش پائینی) این افتوخیزها در حضور مخزن کوچکتر ناپدید میشوند.
شکل ۱) چگالیدهی بوز-انشتین از فوتونها. (قسمت بالا) اشمیت و همکارانس BECای از فوتونی را با پمپاژ اپتیکی که به منظور تحریک مولکولهای رنگی در یک کاواک اپتیکی بکار می رود را تولید کردهاند. این مولکولهای پیرامونی به عنوان یک حمام گرم و یک مخزن ذرات عمل میکنند. (بخش مرکزی) وقتی اندازهی موثر مخزن به حد کافی بزرگ باشد٬ این اسباب شرایط هنگرد بندادی بزرگ را فراهم میکنند. اشمیت و همکارانش افتوخیزهای بزرگی را در تعدادی از ذرات موجود در این چگالیده مشاهده کردهاند. (بخش پائینی) این افتوخیزها در حضور مخزن کوچکتر ناپدید میشوند.
چگالیدههای بوز-انشتین همانند بسیاری از سیستمهایی که حاوی تعدادی زیادی از ذرات هستند٬ به شکل آماری توصیف میشوند. هنگردهای آماری مختلف (تعداد زیادی از ذراتی که تحت شرایط ترمودینامیکی ویژه مهیا میشوند) میتوانند از خواص فیزیکی مشابهی برخوردار باشند. اما نسلهای مختلفی از فیزیکپژوهان بر سر این موضوع بحث کردهاند که چنان رفتاری نبایستی در مورد افتوخیزهای ذرات در چنین چگالیدههایی صادق باشد(۲). بویژه وقتی یک BEC بتواند هم گرما و هم ذرات را با یک مخزن گرمایی تبادل کند(شرایطی که از آن بعنوان «هنگرد بندادی بزرگ» یاد میشود) نظریهپردازان یک افتوخیز «فاجعهبار» را پیشبینی کردهاند. طوریکه افتوخیزها در تعدادی از این ذرات به بزرگی تعداد کل ذرات موجود در چگالیده است. برعکس٬ تحت شرایط «هنگرد بندادی» (که در آن تنها گرما و نه ذرات میتوانند با یک مخزن تبادل شوند) تعداد کل ذرات بایستی پایسته مانده و افتوخیزهای بزرگ رخ نمیدهند. به شکل مشابه٬ افتوخیزهای بزرگ نبایستی در یک هنگرد «میکروکانونی» رخ رهند؛ هنگردی که در آن هم انرژی و هم ذرات پایسته میمانند.
تاکنون فیزیکدانان تجربی این اثرات آماری وابسته به هنگرد در BECها را مشاهده نکرده بودند. یک دلیل عملی بر این ادعا وجود دارد: در مورد یک چگالیدهی اتم٬ گاز اتمی بایستی از محیط پیرامونش ایزوله باشد تا بتوان آن را تا دماهای پایین سرد کرد. بنابراین چنان BECهایی را معمولاً میتوان تحت شرایط هنگرد میکروکاننی ایجاد کرد(۲). در اصل بایستی امکان مشاهدهی افتوخیزهای ذرات در BECهایی از اکسیتون-پلاریتون وجود داشته باشد. چنان چگالیدههایی در سیستمهای حالت-جامد میتوانند رخ دهند. اما٬ هم کنترل صحیحِ مخزن و هم اندازهگیری دقیق افتوخیزهای سریع (در مقیاس پیکوثانیه) به دشواری به اثبات رسیده است. نهایتاً این سوال پیش میآید که آیا امکان این وجود دارد که یک BEC تحت شرایط هنگرد بندادی بزرگ تشکیل شود.
گروه بن نشان دادهاند که در حقیقت این شرایط را میتوان در BECای از فوتونها ممکن ساخت؛ سیستمی که آنها چندین سال پیش تولید کردهاند(۵). در این سیستم٬ فوتونهایی را با استفاده از یک لیزر برای تحریک مولکولهای رنگی در داخل یک کاواک اپتیکی با آینههایی در دو انتهای آن ایجاد کردهاند (شکل ۱ قسمت بالا). اگر این دو آینه کاملاً صاف باشند تنها حرکت فوتونها در جهت طولی (در جهت عمود بر آینهها) کوانتیده شده و فوتونها برای حرکت در جهت عرضی آزاد خواهند بود؛ رفتاری که معادل رفتار فوتونهایی است که جرم موثر دارند. اما آینهها در دستگاه اشمیت و همکارانش اندکی انحنا یافته است. این کار باعث میشود تا محدودشدگی (Confinemet) بیشتری فراهم شود و حتی حرکت عرضی فوتونها نیز کوانتیده گردد. در نتیجه٬ فوتونهای به دام افتاده همچون یک گاز دوبعدی از بوزونهای پرجرم در پتانسیل هارمونیک رفتار میکند. مولکولهای رنگی در آزمایش اشمیت و همکارانش با چنان دقتی انتخاب میشوند که در زمان تحریکشدن٬ فوتونهایی را گسیل کنند که انرژی آنها با انرژی زیرترازهای یک مد طولی کاواک ویژه (در این مورد ۲.۱ الکترونولت) مشابه باشد. برای ایجاد یک BEC ٬ بایستی طول موج دوبروی بوزونها٬ همپوشانی چشمگیری باهم داشته باشند که این اتفاق برای اتمها تنها در دماهای زیرمیکرو کلوین رخ میدهد. اما جرم موثر فوتونهای کاواکِ موردنظر در آزمایش اشمیت و همکارانش چندین مرتبه کوچکتر از اندازهی یک اتم هیدروژن است؛ چیزی که باعث میشود BECی فوتونها در دمای اتاق تشکیل شود.
در این سیستم مولکولهایی که در کاواک حضور دارند قادرند تا فوتونها را هم جذب کنند و هم گسیل. بنابراین هم به عنوان یک مخزن ذره عمل میکنند و هم حمام گرم. گروه بن از اسبابی موسوم به هانبری-براون-توئیس (Hanbury-Brown-Twiss) برای اندازهگیری افتوخیزهای متوسط δn0 حول مقدار میانگین n0 فوتونهای چگالیده استفاده میکنند. پژوهشگران میتوانند نوع مخزن (و از اینرو شرایط هنگردیِ آماری) را تغییر دهند. آنان این کار را با میزانسازیِ تعداد مولکولهای رنگی و تغییر در ترکیب شیمیایی آنها (به منظور تغییر فرکانس گذار این مولکولها) انجام میدهند. در حقیقت این محققان٬ با افزایش اختلاف فرکانس بین فرکانس مولکولهای رنگی و فرکانس مد کاواک٬ جفتشدگی دمایی بین فوتونهای کاواک و مخزن را کاهش میدهند. این پارامترهای کنترلی آنان را قادر میسازد تا اندازهی موثر مخزن را به بیش از سه برابر تغییر دهند. تاثیر اندازهی مخزن بر روی ویژگیهای افتوخیزی جالب است: وقتی ۳۰ درصدِ تمامی فوتونهای درون کاواک چگالیده میشوند و مخزن در بزرگترین حالت خود قرار دارد٬ این پژوهشگران یک تعداد افتوخیز نسبی δn/0n0≃80% (شکل یک- بخش مرکزی) را مشاهده میکنند. این «آشفتگی» بزرگ و غیرعادی برای چنان فاجعهی افتوخیزیِ بندادیِ بزرگ انتظار میرود. اگر آنها اندازهی مخزن را کاهش دهند٬ برای کسر چگالیدهگیِ یکسان٬ افتوخیز نسبی (δn0 /n0) تدریجاً به سمت صفر میرود (شکل یک-بخش پائینی).
همانطور که اشمیت و همکارانش به آن دست یافتهاند٬ توزیع فوتونها در سیستم موردنظر به ازای مخزنی با اندازهی دلخواه٬ با مدل سادهی آماری توافق دارد. یک فرض اصلی برای این مدل آماری (۶) این است که در حالت پایا٬ تعداد مولکولهایی که به شکل اپتیکی تحریک شدهاند (یعنی تعداد فوتونهای داخل مخزن) بعلاوهی فوتونهای داخل کاواک ثابت است. برای آنکه چنین ادعایی صحت داشته باشد٬ بایستی میراییِ تحریکات مولکولی در محلول رنگی پائین باشد؛ همانگونه که در آزمایش اشمیت و همکارانش نیز چنین است. برای یک مخزن به حد کافی بزرگ٬ آمار هنگرد بندادی بزرگ هم در آزمایش و هم در تئوری بدست میآید.
اینکه آیا ممکن است فوتونهایی ساخته شوند که یک BEC واقعی را تشکیل دهند٬ منشا برخی بحثها بوده است. دلیل وجود چنان بحثهایی این است که حتی زمانیکه آینهها در یک کاواک اپتیکیِ بازتابکنندهی بسیار خوب قرار داشته باشند٬ فوتونها طولعمر محدودی دارند. اشمیت و همکارانش برای جبران چنین نقطهضعفی به تحریک مدام فوتونهای جدید در آزمایششان نیاز دارند. در نگاه اول به نظر میرسد یک سیستمی که به شکل مدام پمپاژ میشود نمیتواند هرگز به تعادل گرمایی برسد؛ در مقالاتی که دربارهی تولید نور لیزری فوتونی و چگالش مطالعاتی انجام شده(۷و۸و۹) بر روی این موضوع بحث شده است. اما نظریهی غیرتعادلی اخیر (۹) نشان داده که حداقل برای سیستمهای رنگی (همچون سیستمی که در آزمایش اشمیت و همکارانش استفاده شده) افزایش طولعمر فوتونهای کاواک٬ به تشکیل یک چگالش گرماداده شده و شبه بوز-انشتین از فوتونها میانجامد. نکتهی اصلی این است که فوتونها میتوانند با دمای ارتعاشیِ ناشی از مولکولهای رنگی٬ در طول جذب و بازگسیلِ فوتونهای مکرر به تعادل گرمایی برسند. مادامیکه این فرآیندها سریعتر از زمانی که طول میکشد تا یک فوتون در کاواک میرا شود٬ انجام گردد٬ تعادل گرمایی قابل دسترسی خواهد بود.
اشمیت و همکارانش اساساً «مهندسیِ مخزن» را اجرا کردهاند: این گروه چنان سیستم آزمایشگاهی را طراحی کردهاند که به واسطهی آن به افتوخیزهای یک چگالیدهی بوز-انشتین تسلط پیدا میکنند. فیزیکِ موجود در سیستم آنها را میتوان در دیگر سیستمهای بسذرهای (همچون یک چگالیدهگی اکسیتون-پلاریتون) نیز اعمال کرد. این کار همچنین در درک شرایط غیرتعادلی با آمار غیرحرارتی مفید باشد. مسیر جذابی که میتواند در آینده دنبال شود این خواهد بود که ببینیم برهمکنشهای بین فوتونها در کاواک٬ ویژگیهای آماریِ BEC فوتونی را چگونه تحت تاثیر قرار میدهد. به ویژه٬ این اثرات ممکن است به انتشار ابرشارهی فوتونی و نیز به فیزیکِ سیستمهای فوتونی که قویاً همبسته هستند٬ مربوط شود.

 بازی آنلاین
بازی آنلاین آپلود عکس
آپلود عکس




![[-] [-]](http://www.flashkhor.com/forum/images/collapse.gif)



