از جمله اصولی که در نظریه اصل موضوعی مجموعهها مورد نیاز است اصول موضوعی است که بتوانند وجود مجموعههای جدید را تضمین نموده و مجموعههای جدید را برای ما تولید کنند.
توجه داشته باشید که ما در نظریه اصل موضوعی مجموعهها همه کارها و تعاریفمان بر پایه اصول موضوع است و هر مطلب در مورد مجموعهها یا باید مستقیماً از اصول موضوع باشدیا از این اصول نتیجه شود. تقریباً تمامی اصول موضوع نظریه اصل موضوعی مجموعهها (بجز مثلا اصل موضوع گسترش) از جمله اصولی هستند که به منظور تولید مجموعههای جدید از مجموعههای قبل طرح شده اند. اولین و مهمترین اصول از این اصول مجموعه ساز اصل موضوع تصریح (Axiom of specification) است. توجه داشته باشید که به اصل موضوع تصریح گاهی اصل موضوع زیرمجموعه (Axiom of subset) نیز میگویند.
این اصل به طور ساده بیان می کند هر حکم یا خاصیت معقول در مورد اعضای یک مجموعه، زیرمجموعهای از آن مجموعه را تعیین میکند. حال قبل از بیان دقیق این اصل به یک مثال میپردازیم.
فرض کنید A مجموعه همه مردان باشد. در این صورت جمله (گزاره نما) « x متاهل است. » گزاره نمایی در مورد اعضای A است که برای برخی از عناصر A گزارهای درست و برای برخی دیگر از عناصر A نادرست است. حال با به کار گیری این جمله در مورد اعضای مجموعه A زیرمجموعهای از A تولید می شود که همان « مردان متاهل » است. برای نمایش این زیرمجموعه از مجموعه A از نماد {x متاهل است:x∈A} یا {x متاهل است|x∈A} استفاده میشود. همچنین {x متاهل نیست:x∈A} بر مجموعه مردان مجرد دلالت دارد. به همین صورت مجموعه {پدر x آدم علیهالسلام است|x∈A} مجموعه دو عضوی هابیل و قابیل را مشخص میکند.
متناظر با هر مجموعه A و هر شرط(گزاره نما) (S(x مجموعهای چون B هست که اعضای آن دقیقاً همان عناصری از مجموعه A هستند که در شرط (S(x صدق میکنند.
اصل موضوع گسترش یگانگی مجموعه B را تضمین میکند. در مورد استفاده از اصل موضوع تصریح توجه به این نکته لازم است که برای تعیین و مشخص نمودن یک مجموعه، در نظر گرفتن یک شرط یا خاصیت چون (S(x کافی نمیباشد بلکه باید مجموعه ای باشد که بتوان خاصیت را برای عضوهای آن تعریف کرد. و خلاصه اینکه برای مشخص کردن یک مجموعه کافی نیست وردی بخوانیم، بلکه لازم است مجموعهای در دست داشته باشیم که ورد را برای اعضای آن مجموعه بخوانیم. به این ترتیب از این دیدگاه چیزهایی مانند {x زوج باشد:x} و یا {x متاهل است:x} مجموعه نــمی باشند.
همچنین اگر (S(x یک خاصیت باشد و مطمئن باشیم که مجموعه عناصری که در (S(x صدق میکنند تشکیل یک مجموعه میدهند این مجموعه را با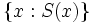 نشان میدهیم. /رشد
نشان میدهیم. /رشد
توجه داشته باشید که ما در نظریه اصل موضوعی مجموعهها همه کارها و تعاریفمان بر پایه اصول موضوع است و هر مطلب در مورد مجموعهها یا باید مستقیماً از اصول موضوع باشدیا از این اصول نتیجه شود. تقریباً تمامی اصول موضوع نظریه اصل موضوعی مجموعهها (بجز مثلا اصل موضوع گسترش) از جمله اصولی هستند که به منظور تولید مجموعههای جدید از مجموعههای قبل طرح شده اند. اولین و مهمترین اصول از این اصول مجموعه ساز اصل موضوع تصریح (Axiom of specification) است. توجه داشته باشید که به اصل موضوع تصریح گاهی اصل موضوع زیرمجموعه (Axiom of subset) نیز میگویند.
این اصل به طور ساده بیان می کند هر حکم یا خاصیت معقول در مورد اعضای یک مجموعه، زیرمجموعهای از آن مجموعه را تعیین میکند. حال قبل از بیان دقیق این اصل به یک مثال میپردازیم.
فرض کنید A مجموعه همه مردان باشد. در این صورت جمله (گزاره نما) « x متاهل است. » گزاره نمایی در مورد اعضای A است که برای برخی از عناصر A گزارهای درست و برای برخی دیگر از عناصر A نادرست است. حال با به کار گیری این جمله در مورد اعضای مجموعه A زیرمجموعهای از A تولید می شود که همان « مردان متاهل » است. برای نمایش این زیرمجموعه از مجموعه A از نماد {x متاهل است:x∈A} یا {x متاهل است|x∈A} استفاده میشود. همچنین {x متاهل نیست:x∈A} بر مجموعه مردان مجرد دلالت دارد. به همین صورت مجموعه {پدر x آدم علیهالسلام است|x∈A} مجموعه دو عضوی هابیل و قابیل را مشخص میکند.
متناظر با هر مجموعه A و هر شرط(گزاره نما) (S(x مجموعهای چون B هست که اعضای آن دقیقاً همان عناصری از مجموعه A هستند که در شرط (S(x صدق میکنند.
اصل موضوع گسترش یگانگی مجموعه B را تضمین میکند. در مورد استفاده از اصل موضوع تصریح توجه به این نکته لازم است که برای تعیین و مشخص نمودن یک مجموعه، در نظر گرفتن یک شرط یا خاصیت چون (S(x کافی نمیباشد بلکه باید مجموعه ای باشد که بتوان خاصیت را برای عضوهای آن تعریف کرد. و خلاصه اینکه برای مشخص کردن یک مجموعه کافی نیست وردی بخوانیم، بلکه لازم است مجموعهای در دست داشته باشیم که ورد را برای اعضای آن مجموعه بخوانیم. به این ترتیب از این دیدگاه چیزهایی مانند {x زوج باشد:x} و یا {x متاهل است:x} مجموعه نــمی باشند.
همچنین اگر (S(x یک خاصیت باشد و مطمئن باشیم که مجموعه عناصری که در (S(x صدق میکنند تشکیل یک مجموعه میدهند این مجموعه را با
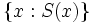 نشان میدهیم. /رشد
نشان میدهیم. /رشد

 بازی آنلاین
بازی آنلاین آپلود عکس
آپلود عکس




![[-] [-]](http://www.flashkhor.com/forum/images/collapse.gif)



