از جمله اصول موضوع نظریه مجموعه های تسرملو-فرانکیل اصل موضوع مجموعه تهی است.
حتما تا به حال با مجموعههای زیادی آشنا شدهاید، مثلاً مجموعه اعداد صحیح یا مجموعه حروف الفبا و ... . میدانید که برای شناختن یک مجموعه کافی است اعضای آن را مشخص کنیم و شما حتما تا به حال این کار را انجام دادهاید. اما ممکن است در این میان یک سوال پیش بیاید و آن این است که آیا مجموعهای وجود دارد که دارای هیچ عضوی نباشد؟ اگر چنین مجموعهای وجود دارد آیا یکتا است یا حداقل دو نمونه از آن وجود دارد؟ این این قسمت به بررسی پاسخ این سوالات میپردازیم.
خوب برای اینکه چیزی در دست داشته باشیم بیاید فرض کنیم مجموعهای وجود دارد و آن را A مینامیم. یکی از اولین نتایج این فرض به ظاهر بیآزار این است که مجموعه بیهیچ عضو وجود دارد. به عبارت دیگر خاصیت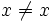 یا هر خاصیت همواره غلط دیگر را برای عناصر مجموعه A به کار بگیرید. برطبق اصل موضوع تصریح،
یا هر خاصیت همواره غلط دیگر را برای عناصر مجموعه A به کار بگیرید. برطبق اصل موضوع تصریح، 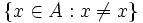 یک مجموعه است و وضوحاً دارای هیچ عضوی نمیباشد. پس مجموعهای بیهیچ عضو وجود دارد همچنین اصل موضوع گیترش یگانگی چنین مجموعهای را تضمین میکند. پس اصل موضوع زیر را داریم:
یک مجموعه است و وضوحاً دارای هیچ عضوی نمیباشد. پس مجموعهای بیهیچ عضو وجود دارد همچنین اصل موضوع گیترش یگانگی چنین مجموعهای را تضمین میکند. پس اصل موضوع زیر را داریم:
دقیقاً یک مجموعه بیهیچ عضو داریم.
دیدن لینک ها برای شما امکان پذیر نیست. لطفا ثبت نام کنید یا وارد حساب خود شوید تا بتوانید لینک ها را ببینید.
اصل موضوع گسترش یگانگی چنین مجموعه ای را تضمین می کند ولذا چنین مجموعه ای شایسته نام و نماد است. مجموعه بی هیچ عضو را مجموعه تهی می نامیم و ان را با {} یا نمایش می دهیم. پس اصل موضوع مجموعه تهی بیان می کند مجموعه تهی وجود دارد.
رای اثبات این مطلب فرض کنید A یک مجموعه دلخواه باشد. اگر تهی زیرمجموعه A نباشد پس حتماً عضوی در تهی وجود دارد که به A تعلق ندارد ولی این امر محال است چون تهی اصلا عضوی ندارد. پس غلط نمیباشد (پس درست است) و لذا تهی زیرمحموعه همه مجموعهها است.
غلط نمیباشد (پس درست است) و لذا تهی زیرمحموعه همه مجموعهها است.
اصل موضوع مجموعه تهی را می توان به نوعی توسط دیدن لینک ها برای شما امکان پذیر نیست. لطفا ثبت نام کنید یا وارد حساب خود شوید تا بتوانید لینک ها را ببینید.
اصل موضوع تصریح نتیجه گرفت. در ابتدا برای آنکه چیزی در اختیار داشته باشیم فرض کنید مجموعه ای وجود دارد. اگر این مجموعه را A بنامیم با استفاده از اصل موضوع تصریح و در نظر گرفت یک گزاره نمای همواره نادرست چون می توان مجموعه را تشکیل داد که چون هیچ x یافت نمی شود که در گزاره نما صدق کند وضوحاً مجموعه مذکور دارای هیچ عضوی نیست.
همطلب اخیر باعث می شود، برخی اصل موضوع مجموعه تهی را به عنوان یک قضیه و نه یک اصل قبول کنند. در این شیوه استدلال فرض وجود حداقل یک مجموعه پذیرفته شده است و لذا می توان وجود مجموعه تهی را به عنوان قضیه نشان داد. /رشد
حتما تا به حال با مجموعههای زیادی آشنا شدهاید، مثلاً مجموعه اعداد صحیح یا مجموعه حروف الفبا و ... . میدانید که برای شناختن یک مجموعه کافی است اعضای آن را مشخص کنیم و شما حتما تا به حال این کار را انجام دادهاید. اما ممکن است در این میان یک سوال پیش بیاید و آن این است که آیا مجموعهای وجود دارد که دارای هیچ عضوی نباشد؟ اگر چنین مجموعهای وجود دارد آیا یکتا است یا حداقل دو نمونه از آن وجود دارد؟ این این قسمت به بررسی پاسخ این سوالات میپردازیم.
خوب برای اینکه چیزی در دست داشته باشیم بیاید فرض کنیم مجموعهای وجود دارد و آن را A مینامیم. یکی از اولین نتایج این فرض به ظاهر بیآزار این است که مجموعه بیهیچ عضو وجود دارد. به عبارت دیگر خاصیت
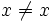 یا هر خاصیت همواره غلط دیگر را برای عناصر مجموعه A به کار بگیرید. برطبق اصل موضوع تصریح،
یا هر خاصیت همواره غلط دیگر را برای عناصر مجموعه A به کار بگیرید. برطبق اصل موضوع تصریح، 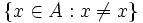 یک مجموعه است و وضوحاً دارای هیچ عضوی نمیباشد. پس مجموعهای بیهیچ عضو وجود دارد همچنین اصل موضوع گیترش یگانگی چنین مجموعهای را تضمین میکند. پس اصل موضوع زیر را داریم:
یک مجموعه است و وضوحاً دارای هیچ عضوی نمیباشد. پس مجموعهای بیهیچ عضو وجود دارد همچنین اصل موضوع گیترش یگانگی چنین مجموعهای را تضمین میکند. پس اصل موضوع زیر را داریم:دقیقاً یک مجموعه بیهیچ عضو داریم.
دیدن لینک ها برای شما امکان پذیر نیست. لطفا ثبت نام کنید یا وارد حساب خود شوید تا بتوانید لینک ها را ببینید.
اصل موضوع گسترش یگانگی چنین مجموعه ای را تضمین می کند ولذا چنین مجموعه ای شایسته نام و نماد است. مجموعه بی هیچ عضو را مجموعه تهی می نامیم و ان را با {} یا نمایش می دهیم. پس اصل موضوع مجموعه تهی بیان می کند مجموعه تهی وجود دارد.
رای اثبات این مطلب فرض کنید A یک مجموعه دلخواه باشد. اگر تهی زیرمجموعه A نباشد پس حتماً عضوی در تهی وجود دارد که به A تعلق ندارد ولی این امر محال است چون تهی اصلا عضوی ندارد. پس
 غلط نمیباشد (پس درست است) و لذا تهی زیرمحموعه همه مجموعهها است.
غلط نمیباشد (پس درست است) و لذا تهی زیرمحموعه همه مجموعهها است.اصل موضوع مجموعه تهی را می توان به نوعی توسط دیدن لینک ها برای شما امکان پذیر نیست. لطفا ثبت نام کنید یا وارد حساب خود شوید تا بتوانید لینک ها را ببینید.
اصل موضوع تصریح نتیجه گرفت. در ابتدا برای آنکه چیزی در اختیار داشته باشیم فرض کنید مجموعه ای وجود دارد. اگر این مجموعه را A بنامیم با استفاده از اصل موضوع تصریح و در نظر گرفت یک گزاره نمای همواره نادرست چون می توان مجموعه را تشکیل داد که چون هیچ x یافت نمی شود که در گزاره نما صدق کند وضوحاً مجموعه مذکور دارای هیچ عضوی نیست.
همطلب اخیر باعث می شود، برخی اصل موضوع مجموعه تهی را به عنوان یک قضیه و نه یک اصل قبول کنند. در این شیوه استدلال فرض وجود حداقل یک مجموعه پذیرفته شده است و لذا می توان وجود مجموعه تهی را به عنوان قضیه نشان داد. /رشد

 بازی آنلاین
بازی آنلاین آپلود عکس
آپلود عکس




![[-] [-]](http://www.flashkhor.com/forum/images/collapse.gif)



