27-03-2020، 23:25
(آخرین ویرایش در این ارسال: 27-03-2020، 23:26، توسط The moon.
دلیل ویرایش: افزودن تصویر/
)
اصل ناوردایی
در اینجا یکی از استراتژی های سطح بالا در حل مسایل را توضیح خواهیم داد. ناوردایی، یک ابزار قدرتمند برای حل مسائل ترکیبیاتی است.
تعریف
هر آنچه که ثابت میماند یک ناوردا است. در واقع ناوردایی عبارت است از تغییر نکردن کمیتها در حین مراحل.
ناوردایی میتواند روی یک چیز خیلی ساده مانند یک عدد تعریف شود. برای مثال فرض کنید در ابتدا عدد ۱ را داریم و در هر مرحله ۲ واحد به آن اضافه کنیم. اینجا یک ناوردایی رخ داده است زیرا این عدد همواره فرد میماند و زوجیت آن در حین مراحل تغییر نمیکند. ناوردایی میتواند روی چیزهای دیگری نیز تعریف شود. رفت و آمد شب و روز یک روند ثابت است و به خودی خود یک ناوردا است. زیاد شدن سن یک فرد یک روند ثابت است و ناورداست.
مسایل این قسمت در نگاه اول مشکل به نظر می رسند اما با حل چند مثال، روش کلی حل مسایل را به دست خواهیم آورد و خواهید دید که گاهی اوقات مسایلی که صورت آنها بسیار پیچیده است، چه باطن ساده ای دارند. در حقیقت روش حل مساله را تنها با حل مساله می توان آموخت. بنابراین توصیه می کنیم پس از مشاهده هر سوال ابتدا سعی کنید خودتان مسایل آن را حل کنید و سپس حل کتاب را مشاهده کنید.
استراتژی اول حل مساله جستجوی قواعد ثابت است. در حل مساله های این فصل این قاعده را رعایت کنید:
اگر یک تکرار مشاهده کردید به دنبال یک قاعده ثابت بگردید.
در مسایل این فصل در هر مساله یک حالت اولیه (فضای ابتدایی) وجود دارد و عملی نیز تعریف شده که در هر گام انجام می شود و معمولاً یک حالت به عنوان هدف نهایی معرفی شده و سوال این است که: آیا می توان به این هدف نهایی رسید یا خیر؟ بنابراین مسایل این فصل 2 حالت دارند:
1.مسایلی که رسیدن به حالت هدف آنها ممکن است: این دسته از مسایل (به نظر من) جالب تر هستند در این مسایل معمولاً به دنبال یک تابع اکیداً صعودی یا اکیداً نزولی برای هر گام می گردیم. پس از یافتن این تابع تقریباً 80% مساله حل شده است. پس از یافتن این تابع معمولاً مسایل به 2 روش حل می شوند.
الف.از آنجا که تابع یکنواست، در گام های مساله به حالت تکراری برنمی خوریم چون بایستی در این صورت رشد تابع در مواقعی به صورت عکس ادامه یافته باشد. اگر تعداد حالت های (فضای) مساله محدود باشد چون در هر گام به یک حالت جدید می رسیم پس این عمل نمی تواند بینهایت بار انجام شود و بالاخره این عمل متوقف می شود و معمولاً توقف عمل معادل حل مساله است.
ب.تابع یکنواست و قدر مطلق رشد آن از مقدار e بیشتر است حالا اگر تابع مورد نظر از مقدار مشخصی بیشتر (یا کمتر) نشود در این صورت این عمل متوقف خواهد شد. در اینجا ذکر یک نکته لازم است. مقدار چرا لازم است: فرض کنید هدف ما عدد 2 است و حالت ابتدا عدد 1 است و در گام اول 1/2 در گام دوم 1/4 در گام سوم 1/8 و ... به عدد 1 اضافه شود مشاهده می کنیم که همیشه می توان به عدد موجود عددی اضافه کرد و هیچ وقت هم این عدد به 2 نمی رسد. اینجا لزوم وجود e اثبات می شود.
2.مسایلی که رسیدن به حالت هدف در آنها ممکن نیست: در این مسایل معمولاً رابطه ثابتی می یابیم که با هر عمل همچنان برقرار باقی می ماند اگر این رابطه برای حالت نهایی (حالت هدف) برقرار نباشد، چون تنها به حالت های ممکن است برسیم که این رابطه را ارضا می کنند، بنابراین به حالت نهایی نمی رسیم (به این روش استفاده از اصل هم خوانی هم می گویند).
یک مثال:
مثال 3
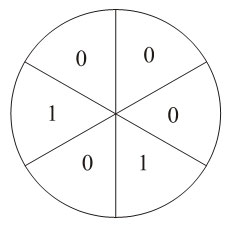
یک دایره را به 6 بخش تقسیم کرده ایم و در جهت خلاف حرکت عقربه های ساعت عددهای 0، 0، 0، 1، 0 و 1 در این بخش ها نوشته ایم. شما می توانید در هر مرحله به دو عدد که در 2 بخش مجاور قرار دارند یک واحد اضافه نمایید. آیا ممکن است به حالتی برسید که تمام اعداد نوشته شده با هم برابر باشند؟
 حل
حل
برای حل مساله فرض می کنیم A مجموع اعداد بخش های اول و سوم و پنجم و B، مجموع اعداد بخش های دوم و چهارم و ششم باشد روشن است که رابطه A-B=2 همیشه برقرار است چون در هر گام به هر یک از A و B یک واحد اضافه می شود. بنابراین امکان ندارد به حالتی برسیم که شش عدد با هم مساوی باشند چون در آن حالت برابر A-B=0 خواهد بود.
در اینجا یکی از استراتژی های سطح بالا در حل مسایل را توضیح خواهیم داد. ناوردایی، یک ابزار قدرتمند برای حل مسائل ترکیبیاتی است.
تعریف
هر آنچه که ثابت میماند یک ناوردا است. در واقع ناوردایی عبارت است از تغییر نکردن کمیتها در حین مراحل.
ناوردایی میتواند روی یک چیز خیلی ساده مانند یک عدد تعریف شود. برای مثال فرض کنید در ابتدا عدد ۱ را داریم و در هر مرحله ۲ واحد به آن اضافه کنیم. اینجا یک ناوردایی رخ داده است زیرا این عدد همواره فرد میماند و زوجیت آن در حین مراحل تغییر نمیکند. ناوردایی میتواند روی چیزهای دیگری نیز تعریف شود. رفت و آمد شب و روز یک روند ثابت است و به خودی خود یک ناوردا است. زیاد شدن سن یک فرد یک روند ثابت است و ناورداست.
مسایل این قسمت در نگاه اول مشکل به نظر می رسند اما با حل چند مثال، روش کلی حل مسایل را به دست خواهیم آورد و خواهید دید که گاهی اوقات مسایلی که صورت آنها بسیار پیچیده است، چه باطن ساده ای دارند. در حقیقت روش حل مساله را تنها با حل مساله می توان آموخت. بنابراین توصیه می کنیم پس از مشاهده هر سوال ابتدا سعی کنید خودتان مسایل آن را حل کنید و سپس حل کتاب را مشاهده کنید.
استراتژی اول حل مساله جستجوی قواعد ثابت است. در حل مساله های این فصل این قاعده را رعایت کنید:
اگر یک تکرار مشاهده کردید به دنبال یک قاعده ثابت بگردید.
در مسایل این فصل در هر مساله یک حالت اولیه (فضای ابتدایی) وجود دارد و عملی نیز تعریف شده که در هر گام انجام می شود و معمولاً یک حالت به عنوان هدف نهایی معرفی شده و سوال این است که: آیا می توان به این هدف نهایی رسید یا خیر؟ بنابراین مسایل این فصل 2 حالت دارند:
1.مسایلی که رسیدن به حالت هدف آنها ممکن است: این دسته از مسایل (به نظر من) جالب تر هستند در این مسایل معمولاً به دنبال یک تابع اکیداً صعودی یا اکیداً نزولی برای هر گام می گردیم. پس از یافتن این تابع تقریباً 80% مساله حل شده است. پس از یافتن این تابع معمولاً مسایل به 2 روش حل می شوند.
الف.از آنجا که تابع یکنواست، در گام های مساله به حالت تکراری برنمی خوریم چون بایستی در این صورت رشد تابع در مواقعی به صورت عکس ادامه یافته باشد. اگر تعداد حالت های (فضای) مساله محدود باشد چون در هر گام به یک حالت جدید می رسیم پس این عمل نمی تواند بینهایت بار انجام شود و بالاخره این عمل متوقف می شود و معمولاً توقف عمل معادل حل مساله است.
ب.تابع یکنواست و قدر مطلق رشد آن از مقدار e بیشتر است حالا اگر تابع مورد نظر از مقدار مشخصی بیشتر (یا کمتر) نشود در این صورت این عمل متوقف خواهد شد. در اینجا ذکر یک نکته لازم است. مقدار چرا لازم است: فرض کنید هدف ما عدد 2 است و حالت ابتدا عدد 1 است و در گام اول 1/2 در گام دوم 1/4 در گام سوم 1/8 و ... به عدد 1 اضافه شود مشاهده می کنیم که همیشه می توان به عدد موجود عددی اضافه کرد و هیچ وقت هم این عدد به 2 نمی رسد. اینجا لزوم وجود e اثبات می شود.
2.مسایلی که رسیدن به حالت هدف در آنها ممکن نیست: در این مسایل معمولاً رابطه ثابتی می یابیم که با هر عمل همچنان برقرار باقی می ماند اگر این رابطه برای حالت نهایی (حالت هدف) برقرار نباشد، چون تنها به حالت های ممکن است برسیم که این رابطه را ارضا می کنند، بنابراین به حالت نهایی نمی رسیم (به این روش استفاده از اصل هم خوانی هم می گویند).
یک مثال:
مثال 3
یک دایره را به 6 بخش تقسیم کرده ایم و در جهت خلاف حرکت عقربه های ساعت عددهای 0، 0، 0، 1، 0 و 1 در این بخش ها نوشته ایم. شما می توانید در هر مرحله به دو عدد که در 2 بخش مجاور قرار دارند یک واحد اضافه نمایید. آیا ممکن است به حالتی برسید که تمام اعداد نوشته شده با هم برابر باشند؟

برای حل مساله فرض می کنیم A مجموع اعداد بخش های اول و سوم و پنجم و B، مجموع اعداد بخش های دوم و چهارم و ششم باشد روشن است که رابطه A-B=2 همیشه برقرار است چون در هر گام به هر یک از A و B یک واحد اضافه می شود. بنابراین امکان ندارد به حالتی برسیم که شش عدد با هم مساوی باشند چون در آن حالت برابر A-B=0 خواهد بود.
source: roshd.ir/ opedia.ir

 بازی آنلاین
بازی آنلاین آپلود عکس
آپلود عکس




![[-] [-]](http://www.flashkhor.com/forum/images/collapse.gif)



